Como os aviões realmente voam?

Antes de explorarmos mais a fundo a física por trás do vôo dos aviões, é importantíssimo entender alguns conceitos prévios.

1. O ar é um fluido. Pode parecer estranho porque estamos acostumados a tratar fluidos como sinônimo de líquidos (como o fluido de freio de um carro). No entanto fluidos são todas as substâncias capazes de se deformar continuamente, não são substâncias rígidas ou cristalinas e possuem a capacidade de “fluir”, como a água em um rio ou a corrente de ar de um ventilador.
2. Devemos abolir a ideia de que aviões voam devido a um único fenômeno físico. É comum vermos explicações que aviões voam por causa do Princípio de Bernoulli, ou por causa do Efeito Coandă, ou por causa da 3ª Lei de Newton (vamos falar sobre eles daqui a pouco). Isso é ser um tanto simplista. É todo o conjunto da obra que faz mais de 40 toneladas de metal sair do chão.

Arrasto aerodinâmico

Como qualquer fluido, o ar gera resistência ao movimento. Chamamos essa resistência de arrasto e, naturalmente, quanto maior a velocidade, maior o arrasto. Podemos entender o arrasto como se fosse uma força em sentido contrário: você está num carro a 120 km/h e o arrasto do ar está tentando te segurar, tentando fazer o carro parar. Quanto mais rápido você se move, mais potência do motor será necessária para tentar vencer o arrasto cada vez maior.

A mesma força de arrasto que gera resistência em um carro é a que gera a sustentação nas asas de um avião. O mesmo ar que tenta te barrar em um carro a 120 km/h é o ar que irá segurar um avião no ar, fazendo-o planar. Basta que a força de sustentação aconteça vindo de baixo, e não de frente.

Antes de falar sobre sustentação, vamos falar sobre o arrasto aerodinâmico:

$$F_a = \frac{1}{2} \rho v^2 C A$$

Isso pode soar bem complexo, mas prometo que é tranquilo. A força de arrasto ($F_a$) é igual à metade da densidade do ar ($\rho$), multiplicado pela velocidade ao quadrado ($v^2$), multiplicado pelo coeficiente de arrasto ($C$, que não vamos precisar nos preocupar no momento), multiplicado pela área da superfície ($A$).

Como você pode ver, é tudo diretamente proporcional. Se eu aumentar a densidade do fluido, aumento o arrasto. Se eu aumentar a velocidade, aumento o arrasto. Se eu aumentar a área da superfície que corta o ar (como um carro de corrida vs. um ônibus), também aumento o arrasto. Mas note algo muito importante: o arrasto aumenta com a velocidade ao quadrado! Se aumento minha velocidade em 2, o arrasto aumenta em 4. Se aumento minha velocidade em 4, o arrasto aumenta em 16. Se aumento minha velocidade em 16, o arrasto aumenta em 256!

A equação da sustentação é praticamente idêntica, pois a mesma força que gera a resistência do ar em um carro na rodovia é a força que segura uma aeronave no ar.

$$L = \frac{1}{2} \rho v^2 C_L S$$

Essa belíssima equação diz que a sustentação ($L$, do inglês, lift) é igual à metade da densidade do ar ($\rho$), multiplicado pela velocidade ao quadrado ($v^2$), multiplicado pelo coeficiente de sustentação ($C_L$, um número que leva em conta o formato da asa, ângulo de ataque, etc.), multiplicado pela área de superfície da asa ($S$). Muito semelhante à outra fórmula que vimos logo antes, não? Mas aqui estamos falando de sustentação, e não de arrasto.

Ao aumentar a velocidade, se aumenta a sustentação. Aumentar a área de superfície da asa, também aumenta a sustentação. Uma maior densidade do ar também traz maior sustentação (por isso aviões no alto de montanhas precisam de mais velocidade para decolar, pois o ar é mais rarefeito). Vamos tentar visualizar essa equação com um experimento mental prático.

Uma folha de papel pesa aproximadamente 4 gramas. Então para fazer um aviãozinho de papel planar, arremessar em uns 2 km/h já é bem suficiente para que a força de sustentação do ar se iguale à força-peso do avião de papel. Se eu fizer um avião de papel-cartão, mais pesado, vou ter que arremessar mais rápido para ele planar, certo? É seguindo esse mesmo princípio que um avião consegue decolar. Um avião pequeno como o Cessna 172 decola a aproximadamente 110 km/h. Um Boeing 787 Dreamliner acelera na pista até aproximadamente 250 km/h para que o ar já tenha força suficiente para tirá-lo do chão.

Aí você pensa: “mas espere, qualquer carro 1.0 alcança 100 km/h, e 250 km/h nem é tão surreal assim!”. Certamente, mas lembre-se que a sustentação aumenta com o quadrado da velocidade. Acelerar de 100 para 200 km/h terá quatro vezes mais sustentação (ou arrasto) do que de acelerar de 0 a 100 km/h.

O fato de o ar ser um gás nos faz subestimar sua força. A água também é mole e podemos facilmente mover nossas mãos calmamente em uma piscina, mas quanto mais rápido você move sua mão, a força necessária para vencer a água aumenta com o quadrado da velocidade até chegar a ponto de te machucar. É bem fácil imaginar uma asa se sustentando ao se mover embaixo d’água, mas como o ar é bem menos denso, preciso compensar com muito mais velocidade.

Aerofólio: o formato especial da asa

Aviões amam voar. O formato e o perfil das asas em forma de gota fazem com que ele, elegantemente, corte o ar sem turbulências e o faça planar. Esse formato se chama aerofólio. Lembre-se de que não importa o peso, pela equação lá em cima basta que se tenha tamanho de asa e velocidade suficiente para sustentá-lo (por isso um avião a jato como um Airbus A320 não consegue voar numa velocidade menor que 200 km/h, mas um avião pequeno de treinamento sim).

Como mencionei no começo do artigo, não é apenas um único fenômeno físico que faz um A380 completamente carregado com mais de 500 toneladas sair do chão. É uma combinação de fatores em seus mais diversos graus de complexidade (tanto conceituais como matemáticos).

Terceira lei de Newton

Um conceito fundamental para pilotagem: aviões não voam perfeitamente na horizontal. Eles voam com o nariz ligeiramente inclinado para cima (entre 2º e 5º no chamado “ângulo de ataque”) para que o ar “bata” na parte de baixo das asas, mantendo-o no ar, semelhante ao que acontece ao colocar suas mãos para fora de um carro numa estrada. Para o avião ganhar altitude numa decolagem, o ângulo é maior ainda: cerca de 15º. Isso acontece devido à 3ª Lei de Newton: para toda força aplicada em um corpo, surge uma força de reação em sentido oposto de igual intensidade.

A frente arredondada (bordo de ataque) e o formato curvo das asas tem dois propósitos: reduzir qualquer turbulência e melhorar a fluidez do ar quando este corta o ar nos mais diversos ângulos; e criar uma região de baixa pressão na parte de cima da asa, otimizando a sustentação.

Efeito Coandă

O perfil curvo da asa faz com que o ar permaneça “colado” na superfície superior da asa (chamada de extradorso), tal como a água de uma torneira aberta escoando por uma colher. A água fará curva, seguirá o formato da colher e você sentirá a colher sendo “puxada” pela água. Esse fenômeno se chama efeito Coandă e é um dos diversos motivos pela qual o avião consegue se sustentar no ar. Se não existisse esse efeito, o ar passaria reto pela asa de forma turbulenta, causando perda de sustentação.

Vale lembrar que o efeito Coandă tem um limite. À medida que o ângulo de ataque aumenta, chega um ponto no qual o fluxo de ar no extradorso se desprende e se torna turbulento. Na aviação isso se chama stall e é extremamente perigoso, pois pode levar à queda do avião.

Princípio de Bernoulli

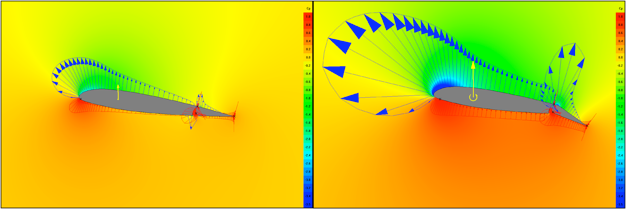
De forma simplista: o efeito Coandă associado ao ângulo de ataque faz com que seja criada uma pequena região de “vácuo” (não é realmente um vácuo, usei a palavra para fins didáticos) no lado superior da asa. O ar do ambiente tentará preencher essa região de baixa pressão, portanto o fluxo de ar se moverá mais rapidamente sobre ela. Este é, basicamente, o princípio de Bernoulli: quanto maior a velocidade de um fluido, menor será sua pressão, e vice-versa.

Podemos representar matematicamente da seguinte forma:

$$p + \rho\frac{v^2}{2} + \rho gh = constante$$

Em um determinado fluido, ao alterar a velocidade ($v$), a pressão ($p$) ou a densidade ($\rho$), o resultado deverá ser sempre constante. Ou seja, se a pressão aumenta, a velocidade deverá diminuir, e vice-versa. Tal como somar 6+6 ou 4+8, se um número aumenta, o outro tem que diminuir para que a soma sempre resulte em 12. Na mecânica dos fluidos, a equação de Bernoulli traduz para os fluidos o princípio de conservação de energia.

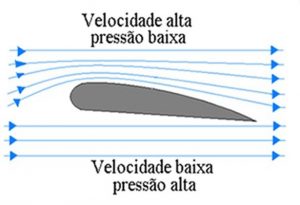
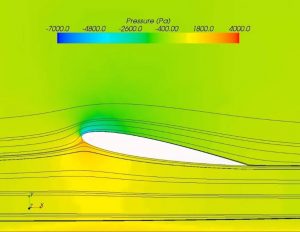
Muitos livros, por motivos de simplificação didática, usam somente o princípio de Bernoulli para explicar o porquê de os aviões voarem. A curva da asa gera uma região de alta pressão no intradorso e uma de baixa pressão no extradorso, gerando sustentação. No entanto, essa lei da física por si só não se justifica, pois deixa algumas pontas soltas:

• Diz-se que o formato curvo da asa cria o gradiente de pressão. Porém, essa regra por si só não explica como um avião de acrobacias ou um caça militar faz voo invertido (voa de cabeça para baixo), e nem explica o voo das asas simétricas (asas que são curvas tanto em cima como embaixo).
• Diz-se que o formato curvo da parte superior da asa tem um caminho mais longo, portanto o ar dividido no bordo de ataque deveria se movimentar mais rapidamente para que eles se encontrem juntos no bordo de fuga (chamada de “teoria do caminho mais longo”). No entanto, não há nada, absolutamente nenhuma lei na física que torne obrigatório o fluxo de ar do intradorso e do extradorso se encontrarem ao mesmo tempo no bordo de fuga da asa. Na realidade, as moléculas de ar na parte superior da asa viajam muito mais rapidamente e atingem o bordo de fuga muito antes.

Apesar do princípio de Bernoulli estar certinho ao explicar a geração da força de sustentação de um avião por meio da diferença de pressão da parte superior e inferior da asa, ele não explica de forma completa. Portanto, a sustentação de um avião não depende somente do princípio de Bernoulli, e sim de todo o conjunto da obra que mencionei no começo do artigo, e dos fenômenos físicos apresentados até o momento.

Flaps: tornando a asa maior

Uma asa de avião não é uma estrutura fixa. Ela possui diversas partes móveis que fazem o avião mudar de direção, levantar ou abaixar o nariz, reduzir a velocidade. No entanto, quando se trata de sustentação aerodinâmica, os flaps são os controles mais importantes para o piloto.

Os flaps ficam na parte de trás da asa do avião. São enormes placas de metal que se estendem para trás e para baixo, tornando a asa mais comprida e mais curva.

Na equação da sustentação do começo do artigo, vemos que para existir sustentação precisamos de velocidade e de área de asa. Quando diminuímos a velocidade, precisamos então aumentar a área da asa para a equação se equilibrar (já que não temos poderes divinos de aumentar a densidade do ar por espontânea vontade), e é aí que entram os flaps. Além da área da asa, os flaps também aumentam sua curvatura e aumentando a pressão do ar na parte inferior, tal como um pássaro curva as asas para frente quando vai pousar. O objetivo dos flaps é aumentar a sustentação da aeronave em baixas velocidades, ou seja, durante pousos e decolagens.

Durante o pouso os flaps ficam em extensão total, pois o objetivo é o avião aterrissar com a menor velocidade possível, poupando os freios e evitando que a aeronave ultrapasse os limites da pista em aeroportos pequenos.

Em contrapartida, os flaps produzem mais arrasto, pois a asa deixa de ser uma superfície completamente lisa. Mais arrasto significa um maior consumo de combustível e um maior stress na estrutura da aeronave. Por esse motivo cada ângulo de flap tem um limite máximo de velocidade. Os flaps são recolhidos aos poucos à medida que o avião vai ganhando velocidade, e estendidos à medida que o avião vai reduzindo a velocidade para o pouso.

Pintando o quadro completo

Os detalhes reais de como uma asa de avião gera sustentação são muito complexos e não se prestam à extrema simplificação. Para um gás, temos que conservar simultaneamente a massa, o momento e a energia no fluxo. As leis do movimento de Newton são declarações relativas à conservação do momento. A equação de Bernoulli é derivada considerando a conservação de energia. Portanto, ambas as equações são satisfeitas na geração de sustentação; ambos estão corretos.

A conservação de massa introduz muita complexidade na análise e compreensão dos problemas aerodinâmicos. Por exemplo, a partir da conservação de massa, uma mudança na velocidade de um gás em uma direção resulta em uma mudança na velocidade do gás em uma direção perpendicular à mudança original. Isso é muito diferente do movimento dos sólidos, no qual baseamos a maioria de nossas experiências na física.

A conservação simultânea de massa, quantidade de movimento e energia de um fluido são chamadas de Equações de Euler (em homenagem a Leonard Euler). Se incluirmos os efeitos da viscosidade, temos as Equações de Navier-Stokes. Para entender verdadeiramente os detalhes da geração de sustentação, é necessário ter um bom conhecimento prático das Equações de Euler.

Mas isso é um papo para outra ocasião.